آموزش رگرسیون لجستیک

سلام من مسعود علی مردی هستم و داخل این پست قصد دارم هرچیزی که در مورد رگرسیون لجستیک میدونم بهتون آموزش بدم. امیدوارم بتونید نهایت استفاده رو ببرید.

در این قسمت قصد داریم که با ارائه یک نمونه مثال و دیتا در SPSS دستور رگرسیون لجستیک را اجرا کنیم. مجموعه داده شامل اطلاعات 999 بیمار مبتلا به کرونا با نتیجه تست PCR مثبت است. در این مثال متغیرهای مورد بررسی شامل وضعیت بیمار (کد یک = بهبود یافته، کد صفر = فوت شده)، سن (کمی و پیوسته)، جنسیت (کد یک = زن، کد صفر = مرد)، بیماری دیابت (کد یک = دارد، کد صفر = ندارد) و بیماری سرطان (کد یک = دارد، کد صفر = ندارد) است. در این مثال متغیر وضعیت بیمار را وابسته و متغیرهای دیگر را به عنوان متغیرهای مستقل در نظر گرفتیم.

جدول توافقی در SPSS

قبل از اجرای دستور رگرسیون لجستیک به منظور بررسی رابطه دو به دوی متغیر وابسته و متغیر­های مستقل کیفی، جداول توافقی و آزمون کای اسکوئر تشکیل می ­شود. برای رسم جداول توافقی از طریق مسیر زیر اقدام می کنیم.

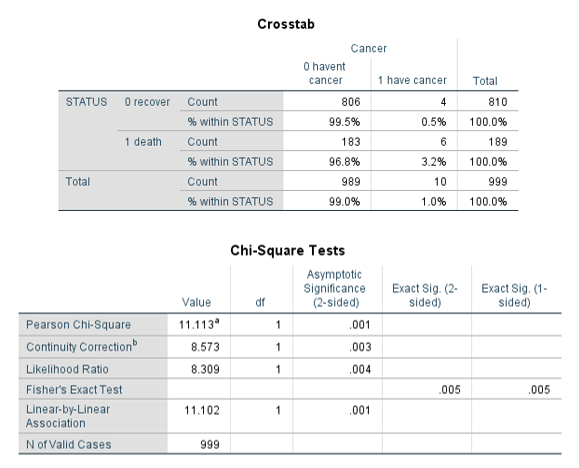
مطابق تصویر زیر متغیر وابسته را به کادر Row و متغیرهای مستقل کیفی را به کادر Column منتقل کرده و از قسمت Statistics تیک گزینه Chi-square را فعال می­ کنیم. خروجی در دو جدول Crosstab و Chi-square Test به دست آمده است که در ادامه آورده شده است.

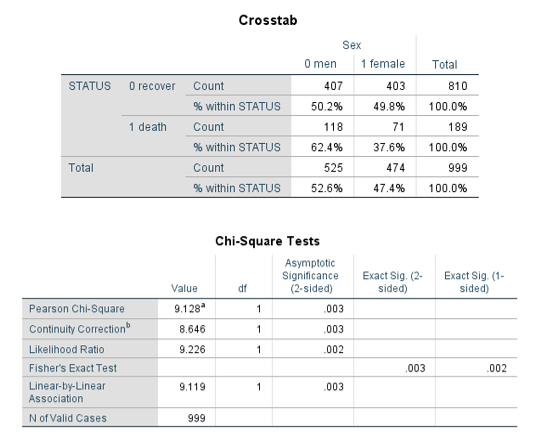
جدول توافقی وضعیت بیمار و جنسیت: بر اساس جدول توافقی 62.4 درصد از مردان و 37.6 درصد از زنان بر اثر ابتلا به کرونا فوت شده ­اند. همچنین سطح معنی داری آزمون کای دو از 0.05 کمتر است بنابراین فرض صفر رد می­شود و دو متغیر وضعیت بیمار و جنسیت در ارتباط هستند.

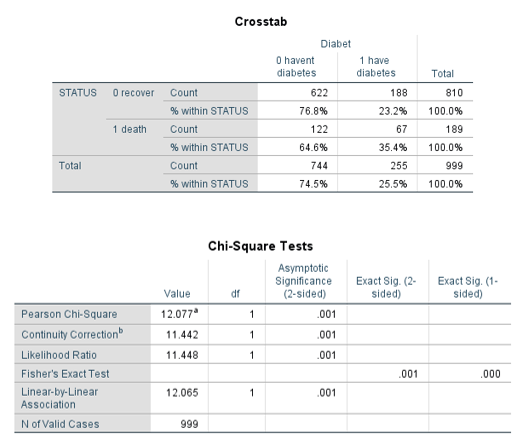
جدول توافقی متغیر وضعیت بیمار و دیابت: بر اساس جدول توافقی 35.4 درصد از بیماران دیابتی بر اثر ابتلا به کرونا دربیمارستان فوت شده­اند و 23.2 درصد از بیماران دیابتی ترخیص شده ­اند. همچنین سطح معنی داری آزمون کای دو کمتر از 0.05 است. بنابراین فرض صفر رد شده و دو متغیر وضعیت بیمار و بیماری دیابت از یکدیگر مستقل نیستند.

جدول توافقی متغیر وضعیت بیمار و سرطان: بر اساس جدول توافقی 3.2 درصد از بیماران سرطانی بر اثر ابتلا به کرونا در بیمارستان فوت شده ­اند. در حالی که 0.5 درصد از بیماران سرطانی ترخیص شده ­اند.

برای اجرای دستور رگرسیون لجستیک در SPSS مسیر زیر را اجرا می کنیم.

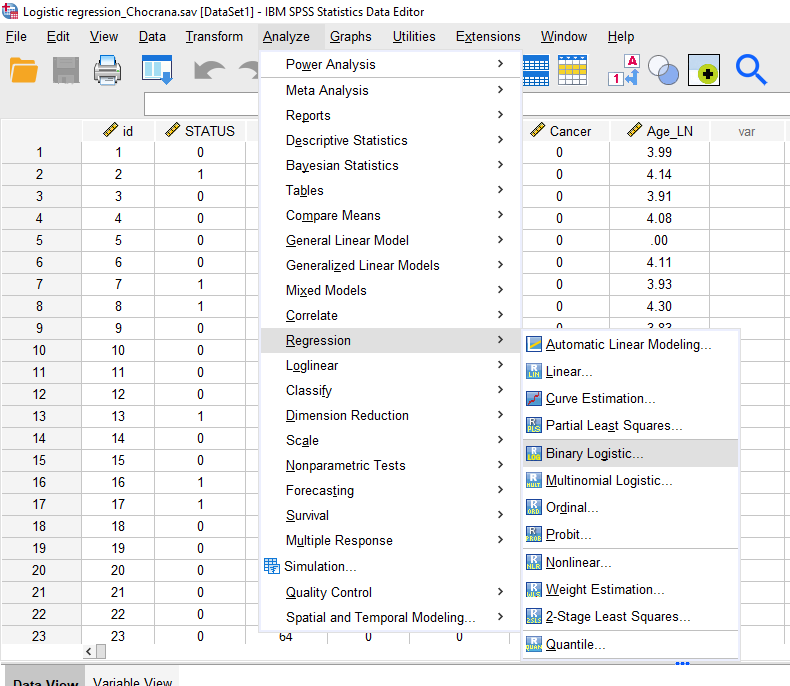
مسیر انجام تحلیل رگرسیون لجستیک در SPSS

با انجام مسیر رگرسیون لجستیک مانند شکل بالا، پنجره زیر باز می شود.

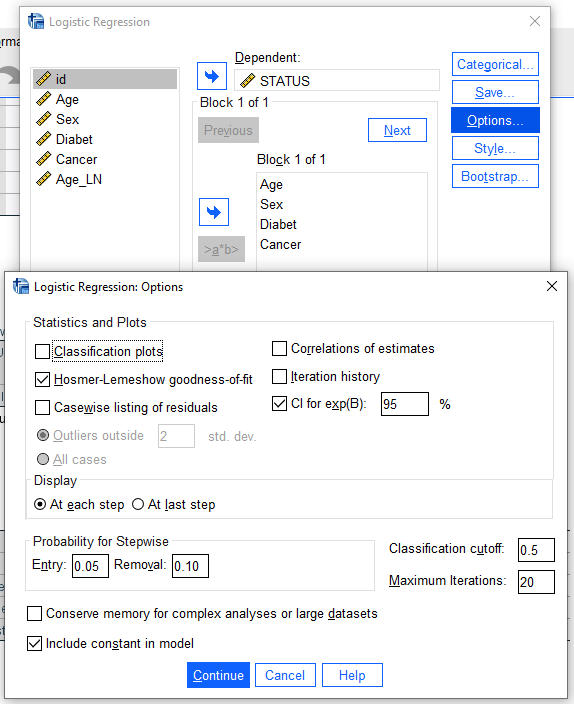
مطابق شکل بالا در پنجره Logistic Regression متغیر وابسته را در کادر Dependent و متغیرهای مستقل را در کادر Covariates قرار می ­دهیم. در ادامه در منوی Options تیک فاصله اطمینان­ ها CI for exp(β) و آزمون Hosmer-Lemeshow را برای بررسی نیکوئی برازش فعال می­ کنیم. سپس بر روی Continue و بعد از آن گزینه Ok کلیک کنید.

تفسیر خروجی های رگرسیون لجستیک در SPSS

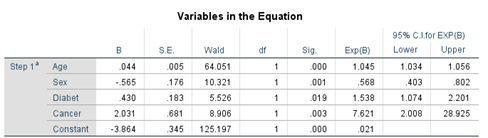
در خروجی نرم افزار SPSS در جدول Variables in the Equation ضرایب مدل رگرسیونی، معناداری، نسبت بخت­ ها و فاصله اطمینان نسبت بخت ­ها قابل مشاهده است.

نسبت بخت ها در رگرسیون لجستیک

به طور متوسط با افزایش یک سال سن بیماران، شانس فوت بیماران بر اثر ابتلا به کرونا پنج درصد افزایش می یابد (OR = 1.05). شانس فوت بر اثر کرونا در زنان 0.57 برابر مردان است، یا به عبارت دیگر، شانس فوت بر اثر کرونا در مردان 75 درصد بیشتر از زنان است (1 تقسیم بر 0.57 می شود 1.75). شانس فوت بر اثر کرونا در بیماران دیابتی 1.54 برابر بیماران غیر دیابتی است، یا به عبارت دیگر شانس فوت بر اثر کرونا در بیماران دیابتی 54 درصد از بیماران غیردیابتی بیشتر است. شانس فوت بر اثر کرونا در بیماران سرطانی 7.62 برابر بیماران غیر سرطانی است.

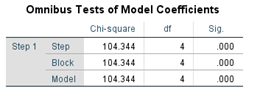
در جدول Omnibus test of model آزمون کلی نگر مورد بررسی قرار می­ گیرد. فرضیه این آزمون معناداری متغیرهای مدل رگرسیونی است. براساس این جدول p – مقدار آزمون از 0.05 کمتر است، بنابراین فرض صفر رد می ­شود و می­ پذیریم مدل رگرسیونی دارای برازش مناسبی است.

در جدول Hosmer and Lemeshow این فرضیه مورد بررسی قرار می ­گیرد که آیا پیشگویی مدل با مشاهدات برابری می­ کند یا خیر. بر اساس جدول p–مقدار آزمون برابر با 72 و از 0.05 بیشتر است، بنابراین دلیلی بر رد فرض صفر وجود ندارد و این آزمون نیز تایید می ­کند که مدل به خوبی برازش داده شده ­است.

در جدول Model Summary آماره منفی دو برابر Log likelihood گزارش شده است. این آماره میزان ضعف پیشگویی مدل در تصمیم گیری را اندازه ­گیری می­ کند. در مقایسه ­ی مدل­ ها هرچه این آماره مقدار کمتری داشته باشد مدل بهتری برازش داده شده است.

انواع رگرسیون لجستیک

رگرسیون لجستیک باینری یا دو سطحی – Binary Logistic Regression

در این مدل رگرسیونی متغیر وابسته به صورت دو سطحی است لذا، تنها دو گروه داریم. مثالی که در بالا ارائه دادیم نمونه ای از یک رگرسیون دو سطحی بود. هدف از طراحی مدل لجستیک این است که با استفاده از یک سری متغیر مستقل پیش بینی انجام دهیم، بطوریکه اگر یک فرد جدید از جامعه ای که مدل سازی را بر اساس اطلاعات نمونه ای این جامعه انجام داده ایم را انتخاب کنیم مدل پیش بینی کند که فرد در کدام طبقه قرار می گیرد.

رگرسیون لجستیک چند سطحی یا چند وجهی – Multinomial Logistic Regression

در این مدل رگرسیونی متغیر وابسته چند وجهی (سه گروه و بیشتر) است. در واقع همانند رگرسیون لجستیک دو وجهی در اینجا نیز می خواهیم بر اساس یکسری از متغیرهای پیشگو، پیش بینی کنیم که یک نمونه جدید بر اساس مدل در کدام یک از گروه ها قرار می گیرد. فرض کنید شغل های موجود در یک جامعه را در چهار گروه طبقه بندی کرده ایم و می خواهیم بررسی کنیم که آیا انتخاب شغل افراد در جامعه می تواند تحت تاثیر سطح تحصیلات آنها و شغل پدارانشان قرار بگیرد.

برای بررسی این موضوع از مدل رگرسیون لجستیک چندسطحی می توان استفاده نمود و متغیر پاسخ در این مثال رده های شغلی که یک متعیر اسمی با چهار سطح است. رگرسیون چند سطحی به طور همزمان تمام جفت گروه ها (گروه رفرنس با سایر گروه ها) را با استفاده ار odds متغیر پاسخ آنها مدل می کند. در این نوع مدل بندی ترتیب گروه بندی اهمیتی ندارد چرا که مدل برای متغیر پاسخ، مقیاس اسمی را در نظر می گیرد.

رگرسیون لجستیک ترتیبی – Ordinal Logistic Regression

زمانی که متغیر پاسخ به صورت ترتیبی می باشد مدل لجستیک می تواند از این ترتیب ها استفاده کند. در نتیجه نتایجی که از مدل لجستیک ترتیبی حاصل می شود به نسبت مدل لجستیک چند سطحی (که متغیر پاسخ را به صورت یک متغیر اسمی در نظر می گیرد) تفسیرپذیرتر و دارای توان آماری بیشتر خواهد بود.

برای مثال یک محقق بازاریابی در یک شرکت می خواهد عوامل تاثیرگذار بر سایز نوشابه (کوچک، متوسط و بزرگ) را که توسط مردم در فست فودهای زنجیره ای سفارش داده می شود مورد بررسی قرار دهد. نوع ساندویج سفارش داده شده، سفارش سیب زمینی سرخ شده و سن مشتریان بعنوان عوامل تاثیرگذار بر سفارش سایز نوشابه است. همانطور که مشخص است متغیر پاسخ (سایز نوشابه)، یک متغیر ترتیبی است.