در این مقاله ضریب همبستگی کندال به صورت تئوری تشریح داده شده و برای آن به صورت دستی و نرم افزاری مثال حل می شود. کندال (M. Kendall 1907-1983) در حدود سال 1930 به مطالعه یک نوع ضریب همبستگی پرداخت که به نام او شهرت دارد. در سال 1948 رساله ای در این باره منتشر کرد که محتوی تئوری این ضریب همبستگی می باشد.در آمار، ضریب همبستگی رتبه‌ای کندال که به تای کندال مشهور است و با حرف یونانی τ نمایش داده می‌شود یک آماره ی ناپارامتری است که برای سنجش همبستگی آماری میان دو متغیر تصادفی به کار می‌رود.
خواص ضریب همبستگی کندال
- از آنجایی که مخرج این کسر تعداد انتخاب‌های زوج‌ها از بین n مشاهده است، همیشه از صورت بزرگتر است. پس ضریب همبستگی کندال از 1 کوچکتر و از 1- بزرگتر است.
- اگر همه زوج‌ها با هم هماهنگ باشند مقدار ضریب همبستگی کندال برابر است با 1.
- اگر همه زوج‌ها ناهماهنگ باشند ضریب همبستگی کندال برابر است با 1-.
- اگر X و Y مستقل باشند، انتظار داریم که ضریب همبستگی کندال نیز برابر با ۰ باشد.
فرمول محاسبه ضریب همبستگی کندال
`T={2S}/{n(n-1)}`
در فرمول فوق n حجم نمونه مورد بررسی می باشد.مقدار S از مجموع اختلاف ui (تعداد داده هایی که بعد از داده ی مورد نظر قرار گرفته و بیشتر از آن است) و vi (تعداد داده هایی که بعد از داده ی مورد نظر قرار گرفته و کمتر از آن است) بدست می آید :
`S=sum_{i=1}^\n d_{i}=sum_{i=1}^\n (u_{i}-v_{i})`
حل مثال دستی ضریب همبستگی Kendall
در جدول زیر نمرات امتحان x و y ده دانش آموز ثبت شده است با استفاده از ضریب همبستگی کندال رابطه بین دو امتحان را محاسبه کنید :
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | دانش آموز |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1 | 6 | 4 | 10 | 7 | 2 | 9 | 3 | 8 | نمره امتحان x |
| 6 | 2 | 4 | 3 | 7 | 8 | 1 | 5 | 10 | 9 | نمره امتحان y |
برای بدست آوردن ضریب همبستگی کندال ابتدا نمرات امتحان x را از کوچک به بزرگ مرتب به صورت زیر مرتب می کنیم و نمرات امتحان y را متقابلا در جدول یادداشت می نماییم :
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | دانش آموز |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | نمره امتحان x |
| 7 | 10 | 9 | 8 | 4 | 6 | 3 | 5 | 1 | 2 | نمره امتحان y |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 1 | vi |
| 0 | 0 | 1 | 2 | 4 | 4 | 6 | 4 | 8 | 8 | ui |
| 0 | 1- | 0 | 1 | 4 | 4 | 6 | 2 | 8 | 7 | di |
محاسبه زوج های هماهنگ و ناهماهنگ
طریقه محاسبه vi بدین صورت است : نمره امتحان y دانش آموز اول را بررسی کرده (برابر 2 است) و به تعدادی که در نمرات سمت راستش کوچکتر از 2 مشاهده کردیم مقدار ui مشخص می شود (در امتحان y فقط نمره دانش آموز دوم از دانش آموز اول کمتر است) پس مقدار 1 اختیار می کند. برای دانش آموز دوم نیز که نمره امتحان y آن برابر 1 است مشاهده می شود که هیچکدام از دانش آموزان بعدی نمره کمتری از او نگرفته اند، لذا مقدار vi برای دانش آموز دوم برابر صفر می باشد.
طریقه محاسبه ui بدین صورت است : نمره امتحان y دانش آموز اول را بررسی کرده (برابر 2 است) و به تعدادی که در نمرات سمت راستش بزرگتر از 2 مشاهده کردیم مقدار vi مشخص می شود (در امتحان y فقط نمره دانش آموز دوم از دانش آموز اول کمتر است) پس مقدار 8 اختیار می کند (اگر بشماریم نمره y دانش آموز اول از 8 دانش آموز بعدی کمتر است). برای دانش آموز دوم نیز که نمره امتحان y آن برابر 1 است مشاهده می شود که هیچکدام از دانش آموزان بعدی نمره کمتری از او نگرفته اند، لذا مقدار vi برای دانش آموز دوم نیز برابر 8 می باشد (فقط نمرات دانش آموزان سمت راست باقی مانده را در شمارش به حساب می آوریم). در انتها مقدار S به صورت زیر بدست می آید :
`S=sum_{i=1}^\10 d_{i}=sum_{i=1}^\10 (u_{i}-v_{i})=31`
`T={2S}/{n(n-1)}={2*31}/{10(9-1)}=0.689`
حل مثال همبستگی کندال در SPSS
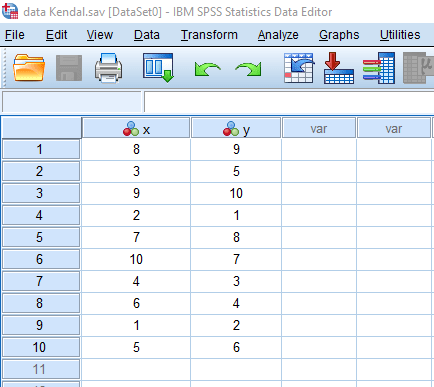
ابتدا به شکل زیر داده ها را وارد نرم افزار SPSS می کنیم : برای دریافت آموزش نحوه ورود داده ها در نرم افزار SPSS اینجا کلیک کنید.
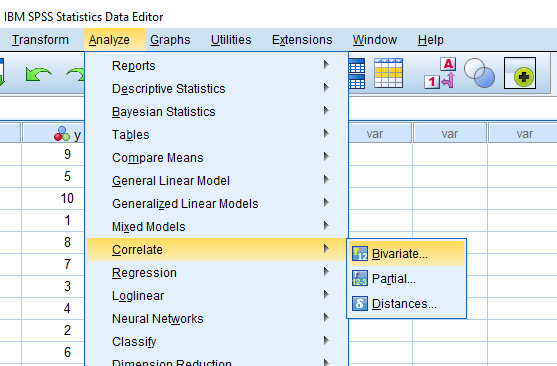
سپس از طریق دستور زیر کادر آزمون ضریب همبستگی میان دو متغیر را باز می کنیم :
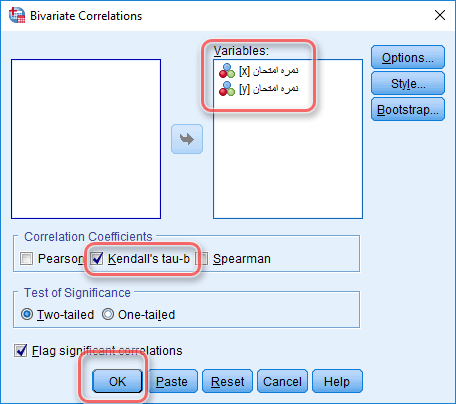
مانند شکل زیر در پنجره باز شده دو متغیر مورد نظر را وارد کادر Variables کنید و تیک ضریب همبستگی تاو-کندال را فعال نمایید، در انتها بر روی گزینه OK کلیک نمایید :
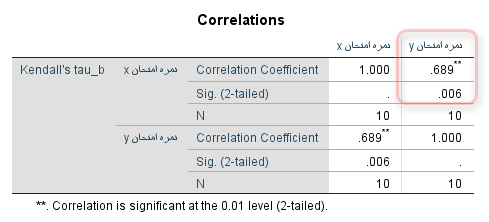
خروجی نرم افزار SPSS برای ضریب همبستگی کندال (KENDALL CORRELATION COEFFICIENTS) به صورت زیر است :
همانطور که مشاهده می شود مقدار ضریب همبستگی برابر با 0.689 بدست آمده است که سطح معنی داری آن با توجه به این که کمتر از 0.05 است نشان از معنی داری این ضریب می باشد.
سلام
خیلی ممنون از مقاله جامع و مفیدی که نوشتید.
آیا وقتی که تعداد نمونه کم باشه فقط باید از کندال استفاده کنیم یا استفاده از پیرسون هم بلامانع است؟
سپاس
سلام و عرض ادب، ممنون از حسن توجه جنابعالی
بله در صورت نرمال بودن داده ها بلامانع است.
سلام
ممنون از مطالب خوبتون
تفاوت کندال و پیرسون رو ممنون میشم مختصرا بگید
مثلا برای داده ای چرا کندال استفاده شده و پیرسون استفاده نشده؟
سلام. ممنون از توجه شما
قبل از انتخاب نوع همبستگی می بایست به مواردی که خدمتتون عرض می کنم توجه بفرمایید.
اگر داده های کمی (فاصله ای یا نسبتی) بودند و همچنین توزیع هر دو متغیر نرمال بود ضریب همبستگی پیرسون می بایست استفاده بشه. اما گاها متغیر های موردنظر کمی (فاصله ای یا نسبتی) می باشند اما توزیع آنها نرمال نمی باشد در این صورت می بایست از ضریب همبستگی کندال استفاده بشه.
از همه مهمتر زمانی که داده ها ماهیت رتبه ای دارند و کمی (فاصله ای یا نسبتی) نیستند می بایست حتما از ضریب همبستگی کندال استفاده بشه.
زمانی هم که حجم نمونه هاتون کمه مثلا در هر متغیر کمتر از ۶ مورد، بهتره که از ضریب کندال استفاده بشه.
سلام خیلی ممنون از اطلاعات عالی ای که به اشتراک گذاشتین، سوالی داشتم از منوی crosstabs برای اینکه جدول توافقی را داشته باشیم و هردو ترتیبی هستند برای اینکه درصد را در جدول داشته باشیم بهتره کدام درصد را فعال کنیم؟ ردیف ،ستون یا کل؟ و نحوه تحلیل به چه صورت خواهد بود؟
ممنونم از پاسخگویی
عرض سلام و احترام؛
این که از کدام درصد استفاده کنید بستگی به خودتان دارد که نتیجه کدام برایتان مهم تر است.
در نهایت از طریق سطح معنی داری متوجه می شوید که دو متغیر مورد نظر از هم مستقل هستند یا رابطه دارند.
سلام
خدا قوت
ضمت تشکر از زحمات و لطف شما در ارایه رایگان اطلاعات . من پرسشنامه ای به دویست و بیست گویه داشته ام که در طیف هفت تایی طراحی شده و ضریب کندال ان را یک نفر افرادی که به اصلاح آمار کار می کردند گرفتند.ضریب کندال بین ۰٫۴۱۲ درصد شده است. به همین دلیل دوباره ضریب لاوشه گرفتند. الان برای نوشتن مقاله isi مشکل دارم. نمیدونم باید فقط ضریب لاوشه را بیاورم یا هر دو را بنویسم.
سلام برای حل مشکل از طریق راه های ارتباطی اعلام شده در خدمت هستم.
دمت گرم داداش. اجرت با خدا