مفهوم خودهمبستگی سریالی مانده های رگرسیون

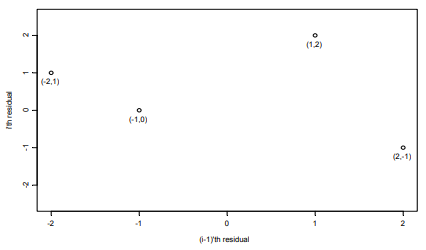
در کارهای رگرسیونی فرض می شود که خطاهای مشاهده شده دو به دو ناهمبسته هستند. اگر این فرض در اصل درست نباشد، انتظار خواهیم داشت که نمودار مانده ها در برابر ترتیب زمان، برای آشکار شدن عدم برقراری این فرض، ما را کمک کند. به رابطه همبستگی یك متغیر با يک دوره قبل خود، خود همبستگی مرتبه اول گویند. خودهمبستگی سریالی رابطه بین متغیر داده شده با خود ولی با یک وفقه در فواصل زمانی مختلف می باشد. همبستگی سریالی (با یک وقفه) می تواند با ترسیم هر مانده به غیر از اولین مانده در برابر مانده‌ی قبل خود مورد بررسی قرار می‌گیرد. برای مثال می توانیم نمودار i امین مانده را در مقابل i-1 امین مانده رسم کنیم به طوری که اگر باقی مانده ها (2-)، (1)، (2)، (1-)، (0) باشند آنگاه نمودار به شکل زیر رسم می شود.

نمودار (1) نمونه ای از رسم نمودار خودهمبستگی مانده ها

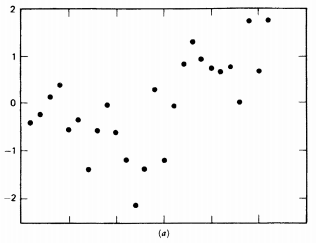
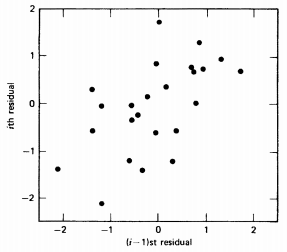
نمودار (2) و (3) تمایل از پایین سمت چپ به بالا سمت راست نقاط را نشان می دهد. (همبستگی مثبت)

زمانی که خودهمبستگی مثبت است :

واریانس کمتر از حد برآورد می‌شود.

خطای نوع اول افزایش می‌یابد.

آماره تی به صورت کاذب افزایش می‌یابد.

نمودار (2) نمونه ای از خودهمبستگی سریالی مثبت

نمودار (3) نمونه ای از خودهمبستگی سریالی مثبت

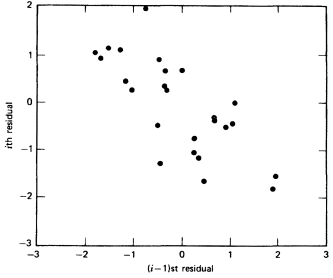
نمودار (4) تمایل از بالا سمت چپ به پایین سمت راست نقاط را نشان می دهد (همبستگی منفی).

زمانی که خودهمبستگی منفی است :

واریانس بیش از حد برآورد می‌شود.

خطای نوع دوم افزایش می‌یابد.

آماره تی کمتر نشان داده می‌شود.

نمودار (4) نمونه ای از خودهمبستگی سریالی منفی

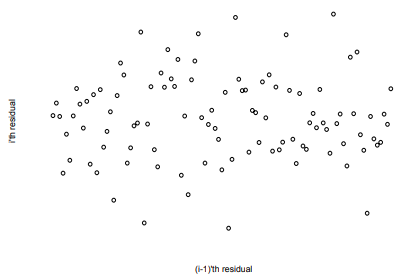
نمودار (5) که روند خاصی در نقاط آن مشاهده نمی شود عدم وجود خودهمبستگی سریالی را نشان می دهد.

نمودار (5) نمونه ای از عدم وجود خوهمبستگی سریالی